Como trabajan los Algoritmos

SHA-1

NIST presentó en 1993 un algoritmo basado en las mismas técnicas que MD5 y denominado SHA (Secure Hash Algorithm).

El primer miembro de la familia fue publicado en 1993 es oficialmente llamado SHA. Sin embargo, hoy día, no oficialmente se le llama SHA‐0 para evitar confusiones con sus sucesores. Dos años más tarde el primer sucesor de SHA fue publicado con el nombre de SHA‐1.

Este algoritmo en 1995 la Agencia de Seguridad Nacional (NSA) lo sustituyó por una versión mejorada que actualmente se conoce como SHA-1 y que se considera más seguro que MD5. Produce un código hash de 160 bits para mensajes de longitud máxima 264 bits, aunque existen otras variantes poco utilizadas todavía que producen códigos de mayor longitud.

En general, SHA1 se considera el mejor algoritmo de la familia de Algoritmos HASH o de resumen y es el que se aplica en la mayoría de las aplicaciones de firma electrónica. Por lo tanto es muy habitual aplicar SHA1 seguido de RSA para realizar una firma electrónica de un documento, o bien el algoritmo DSA específico para firma  electrónica que también utiliza SHA1 internamente.

Ejemplo de hashes

Estos son ejemplos de SHA-1 digiere. ASCII codificación se utiliza para todos los mensajes.

SHA1 (” El rápido zorro marrón salta sobre el perro perezoso “) = 2fd4e1c6 7a2d28fc ed849ee1 bb76e739 1b93eb12

Incluso un pequeño cambio en el mensaje, con una probabilidad abrumadora, resultando en un hash completamente diferente debido al efecto avalancha.

La codificación hash vacía para SHA‐1 corresponde a:

SHA1(“”) = da39a3ee5e6b4b0d3255bfef95601890afd80709

Es imposible encontrar un mensaje que se corresponde con un determinado mensaje.

Es imposible encontrar dos diferentes mensajes que producen el mismo mensaje.

Si un mensaje se cambia incluso de un solo carácter, el resultado será un mensaje totalmente diferente.

SHA‐0 y SHA‐1 producen una salida resumen de 160 bits (20 bytes) de un mensaje que puede tener un tamaño máximo de 264 bits, y se basa en principios similares a los usados por el profesor Ronald L. Rivest del MIT en el diseño de los algoritmos de resumen de mensaje MD4 y MD5.

El procesamiento consta de cinco pasos los cuales se explican a continuación:

Se incorporan bits de relleno al mensaje de entrada de tal modo que cumpla:

El relleno consiste en un uno seguido de los ceros que sean necesarios. Aunque el mensaje ya tenga la longitud deseada, se debe efectuar el relleno, por lo que el número de bits de dicho relleno está en el rango de 1 a 512 bits.

A la salida del paso 1, se le añade un bloque de 64 bits que represente la longitud del mensaje original antes de ser rellenado.

Se inicializa la memoria temporal MD, la cual consta de 160 bits y su finalidad es almacenar los resultados intermedios y finales de la función de dispersión. La MD consta de 5 registros (A,B,C,D,E) de 32 bits cada uno, los valores con los que se inicializan son los siguientes (valores hexadecimales):

A=67452301

B=EFCDAB89

C=98BADCFE

D=10325476

E= C3D2E1F0

4.Se procesa el mensaje por bloques de 512 bits, cada uno pasa por un módulo que consta de 4 rondas de procesamiento de 20 pasos cada una. Las rondas tienen una estructura similar, con la excepción de que cada una ocupa una función lógica primitiva diferente (f1, f2, f3 y f4).

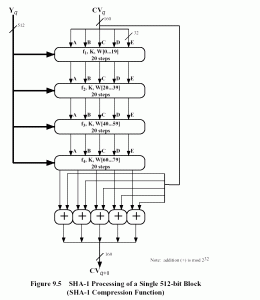
5.- Una vez que se procesan los L bloques de 512 bits, el resumen del mensaje son los 160 bits de salida del último bloque.

SHA‐1 tiene estas propiedades y, por tanto, a que se refiere como seguro. Está diseñado para trabajar con el Algoritmo de Firma Digital (DSA). SHA‐1 es una forma de función de hash.

Funciones en un solo sentido se caracterizan por dos propiedades. La primera es que son de sentido único. Esto significa que usted puede tomar un mensaje y calcular un valor de hash, pero no se puede tomar un valor hash y recrear el mensaje original. También es libre de colisión y, por tanto, no hay dos mensajes hash con el mismo valor.

Aplicaciones de SHA‐1

SHA‐1 puede ser usado en una variedad de aplicaciones:

1. Aplicaciones de seguridad que requieren autenticación

2. E‐mail

3. Transferencia electrónica de fondos

4. Distribución de software

5. Almacenamiento de datos

SHA‐1 ha sido examinado muy de cerca por la comunidad criptográfica pública, y no se ha encontrado ningún ataque efectivo. No obstante, en el año 2004, un número de ataques significativos fueron divulgados sobre funciones criptográficas de hash con una estructura similar a SHA‐1; lo que ha planteado dudas sobre la seguridad a largo plazo de SHA‐1.

RSA

El sistema criptográfico con clave pública RSA es un algoritmo asimétrico cifrador de bloques, que utiliza una clave pública, la cual se distribuye (en forma autenticada preferentemente), y otra privada, la cual es guardada en secreto por su propietario.

Una clave es un número de gran tamaño, que una persona puede conceptualizar como un mensaje digital, como un archivo binario o como una cadena de bits o bytes.

Cuando se envía un mensaje, el emisor busca la clave pública de cifrado del receptor y una vez que dicho mensaje llega al receptor, éste se ocupa de descifrarlo usando su clave oculta.

Los mensajes enviados usando el algoritmo RSA se representan mediante números y el funcionamiento se basa en el producto de dos números primos grandes (mayores que 10100) elegidos al azar para conformar la clave de descifrado.

Emplea expresiones exponenciales en aritmética modular.

La seguridad de este algoritmo radica en que no hay maneras rápidas conocidas de factorizar un número grande en sus factores primos utilizando computadoras tradicionales.

La computación cuántica podría proveer una solución a este problema de factorización.

El algoritmo RSA es un algoritmo de clave pública desarrollado en 1977 en el MIT por Ronald Rivest, Adi Shamir y Leonard Adelman.

Fue registrado el 20 de Septiembre de 1983. El 20 de Septiembre del 2000, tras 17 años, expiró la patente RSA, pasando a ser un algoritmo de dominio público.

Este popular sistema se basa en el problema matemático de la factorización de numeros grandes.

El algoritmo RSA funciona de la siguiente manera:

Inicialmente es necesario generar aleatoriamente dos números primos grandes, a los que llamaremos p y q.

A continuación calcularemos n como producto de p y q: n = p * q

Se calcula fi: fi(n)=(p-1)(q-1)

Se calcula un número natural e de manera que MCD(e, fi(n))=1 , es decir e debe ser primo relativo de fi(n).

Es lo mismo que buscar un numero impar por el que dividir fi(n) que de cero como resto.

Mediante el algoritmo extendido de Euclides se calcula d: e.d mod fi(n)=1 Puede calcularse d=((Y*fi(n))+1)/e para Y=1,2,3,… hasta encontrar un d entero.

El par de números (e,n) son la clave pública.

El par de números (d,n) son la clave privada.

Cifrado: La función de cifrado es C = M^e mod n

Descifrado: La función de descifrado es M = C^d mod n

Ejemplo con números pequeños

Escogemos dos números primos, por ejemplo p=3 y q=11.

n = 3 * 11 = 33

fi(n) = (3-1) * (11-1) = 20

Buscamos e: 20/1=0, 20/3=6.67. e=3

Calculamos d como el inverso multiplicativo módulo z de e, por ejemplo, sustituyendo Y por 1,2,3,… hasta que se obtenga un valor entero en la expresión: d = ((Y * fi(n)) + 1) / e = ( Y * 20 + 1) / 3 = 21 / 3 = 7

e=3 y n=33 son la clave pública

d=7 y n=33 son la clave privada

Cifrado: Mensaje = 5, C = M^e mod n = 5^3 mod 33 = 26

Descifrado: M = C^d mod n = 26^7 mod 33 = 8031810176 mod 33 = 5

Ejemplo visual de RSA

Un ejemplo pedagógico trivial del algoritmo RSA se muestra en la siguiente animación. Para este ejemplo hemos seleccionado p=3 y q=11, dando n=11 y z=20. Un valor adecuado de d es d=7, puesto que 7 y 20 no tienen factores comunes.

Con estas selecciones, e puede encontrarse resolviendo la ecuación 7e=1(mod 20), que produce e=3.El texto cifrado, C, de un mensaje de texto normal, P, se da por la regla C=P3(mod 33). El texto cifrado lo descifra el receptor de acuerdo con la regla P= C7(mod 33). Observe la animación tanto en el emisor como en el receptor, donde se muestra el cifrado-descifrado del texto normal “CASA”.

Dado que los números primos escogidos para este ejemplo son tan pequeños, P debe ser menor que 33, por lo que cada bloque de texto normal puede contener sólo un carácter. El resultado es un cifrado por sustitución monoalfabética, no muy impresionante. En cambio si hubiéramos seleccionado p y q  10100, podríamos tener n  10200, para que cada bloque pueda ser de hasta 664 bits (s644 10200) u 83 caracteres de 8 bits, contra 8 caracteres para el DES.

 MD5

El algoritmo de hash más utilizado en estos momentos es el MD5 . Este algoritmo fue desarrollado por Ronald Rivest en 1995 y está basado en dos algoritmos anteriores MD2 y MD4. Todos estos protocolos producen un número de 128 bits a partir de un texto de cualquier longitud.

MD4 fue desarrollado para mejorar el rendimiento de MD2 , sin embargo, varios problemas fueron detectados y en 1996 fueron publicados elementos que hacen hoy en día inservible el algoritmo. MD5 sustituyó a MD4 y aunque no tiene el rendimiento de su antecesor, hasta el momento no han sido publicados elementos que comprometan su integridad y funcionamiento.

MD5 comienza rellenando el mensaje a una longitud congruente en módulo 448 mod 512. Es decir la longitud del mensaje es 64 bits menos que un entero múltiplo de 512. El relleno consiste en un bit en 1 seguido por cuentos bits en 0 sean necesarios. La longitud original del mensaje es almacenada en los últimos 64 bits del relleno.

Adicionalmente se inicializa, con un valor fijo, un buffer de 128 bits. Este buffer puede verse

como 4 registros de 32 bits (A,B,C,D) y son inicializados con los siguientes valores hexadecimales:

A=67452301; B=EFCDAB89; C=98BADCFE; D=10325476

Durante varias rondas de procesamiento el algoritmo toma bloques de 512 bits de la entrada y los mezcla con los 128 bits del buffer. Este proceso es repetido hasta que todos los bloques de entrada han sido consumidos. El valor resultante en el buffer es el hash del mensaje.

MD5 no es el único algoritmo de hash conocido. Existe otra función llamada Secure Hash Algorithm, (SHA), desarrollado por NSA.. A diferencia de MD5, SHA genera números hash de 160 bits.